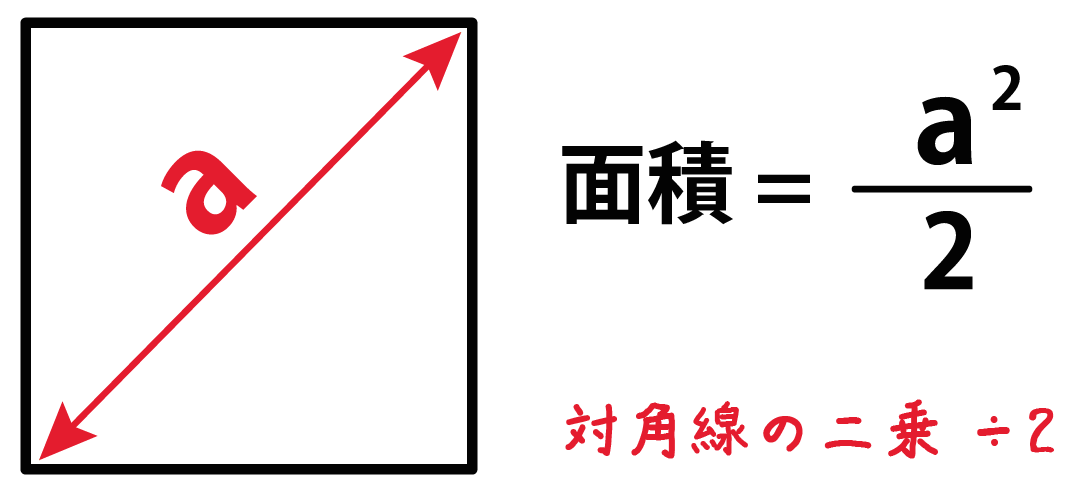
簡単公式 対角線で正方形の面積を3秒で計算できる求め方 Qikeru 学びを楽しくわかりやすく
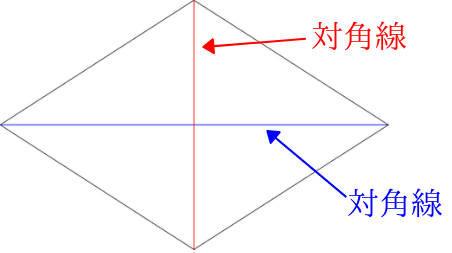
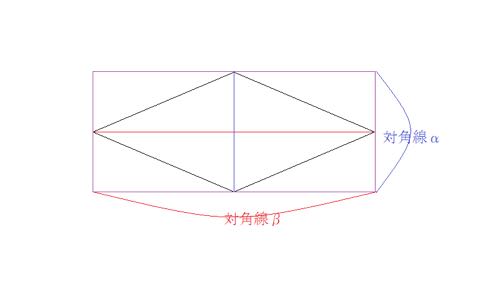
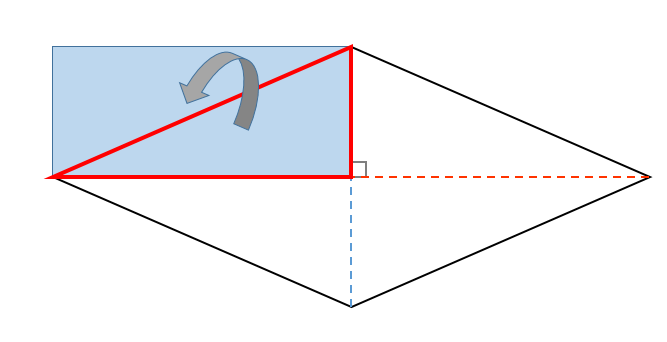
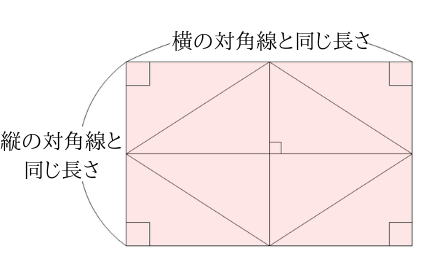
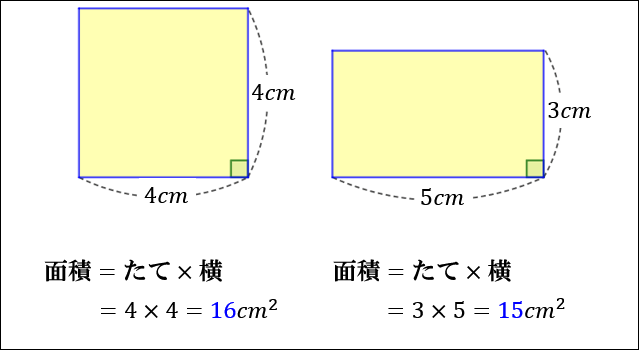
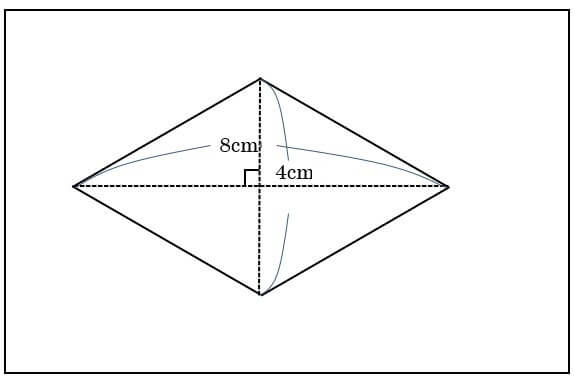
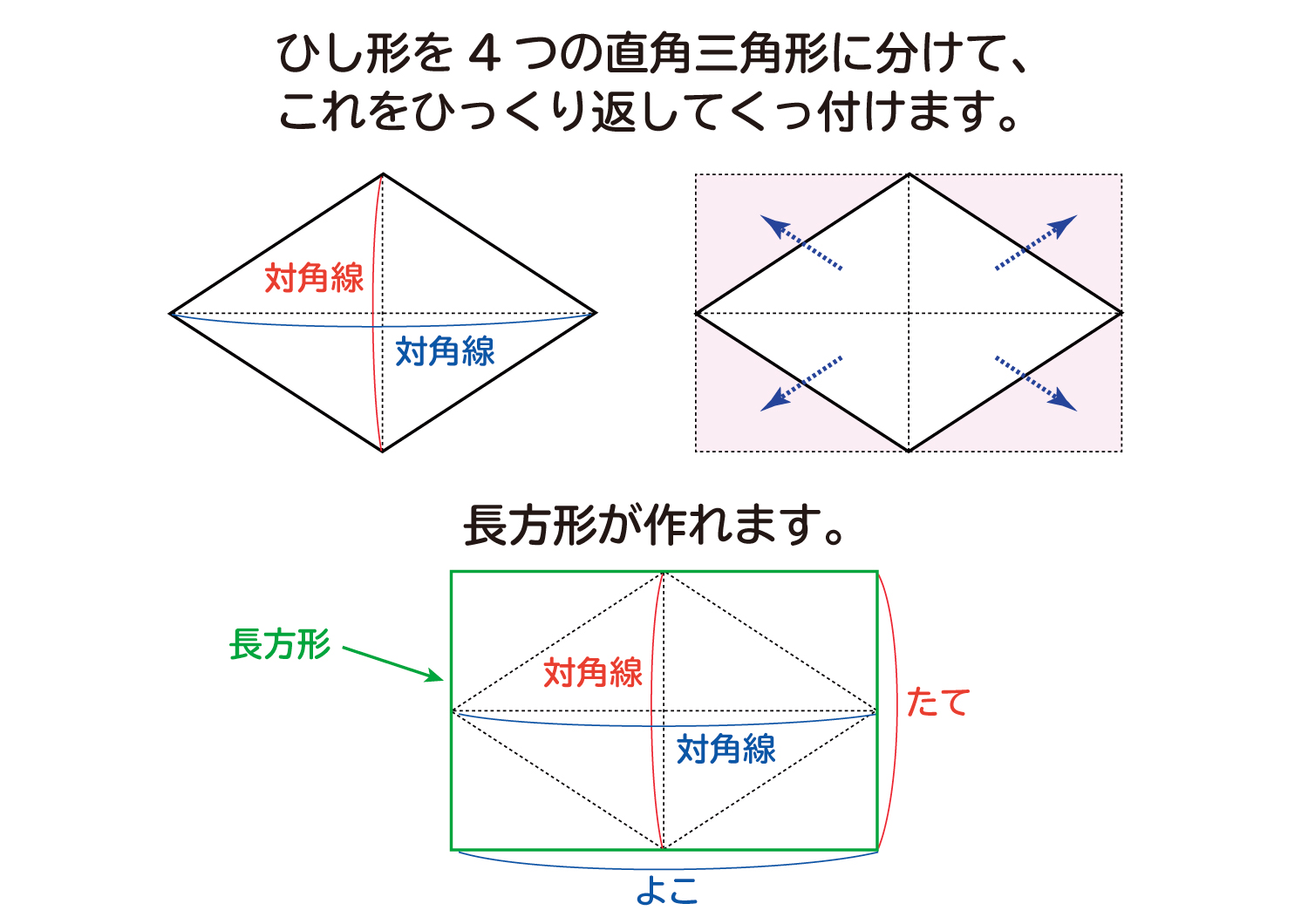
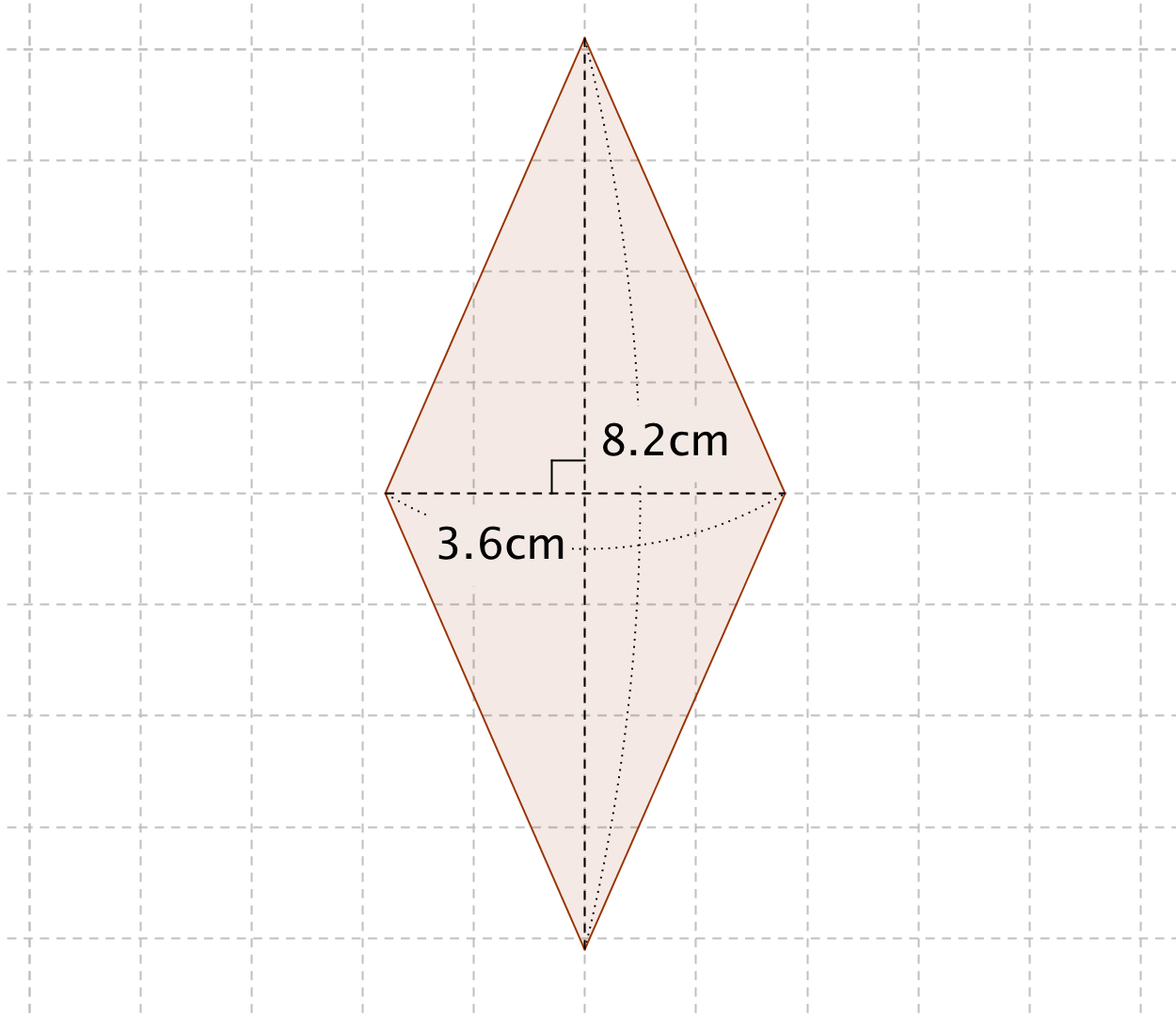
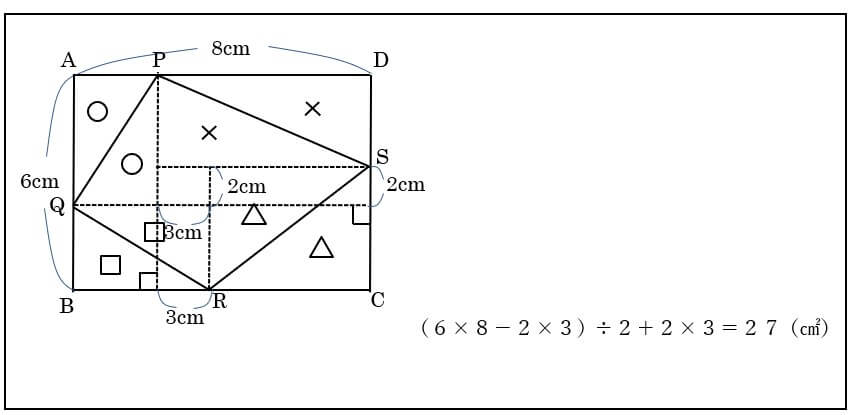
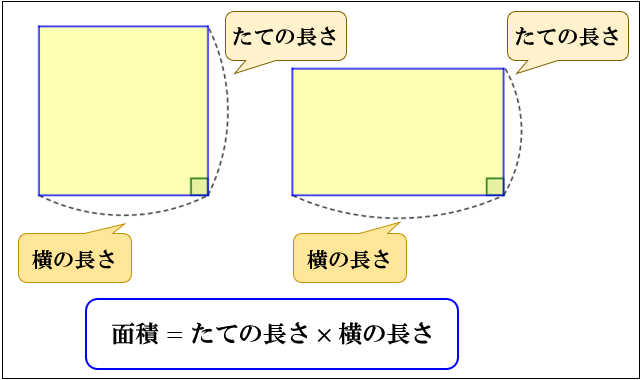
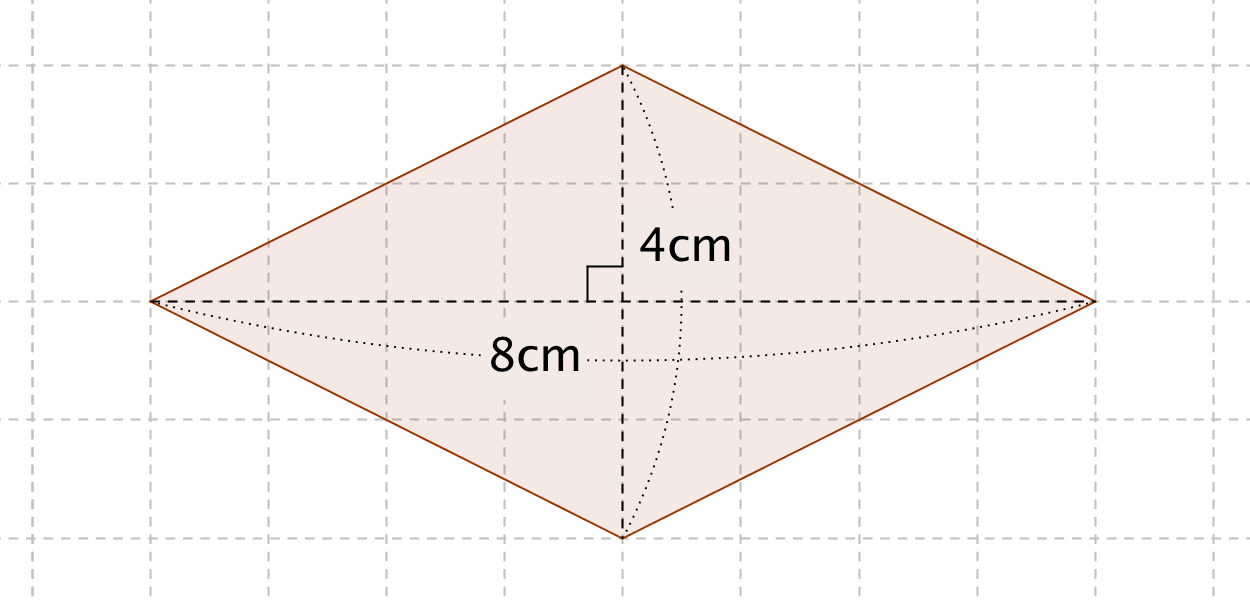
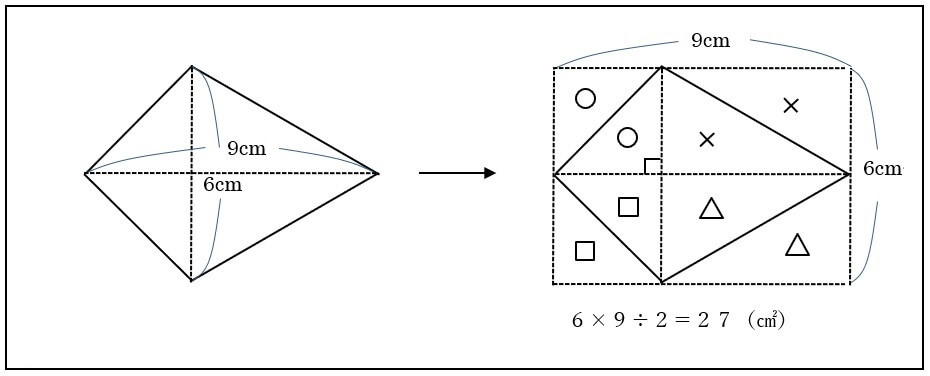
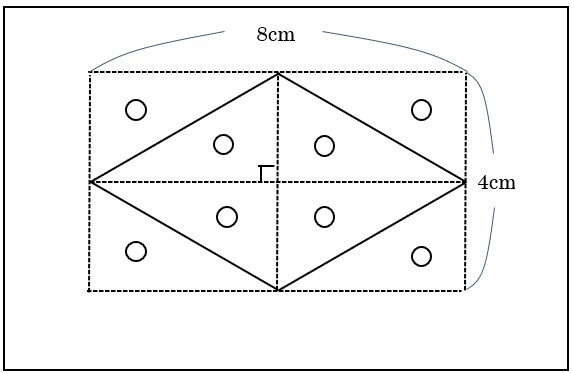
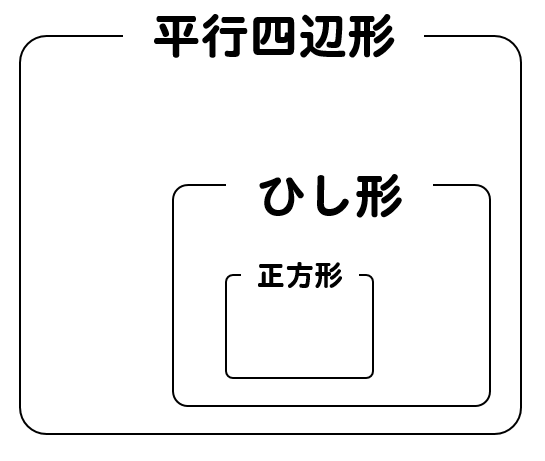
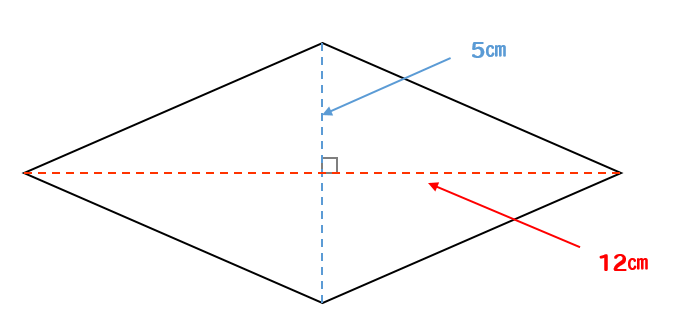
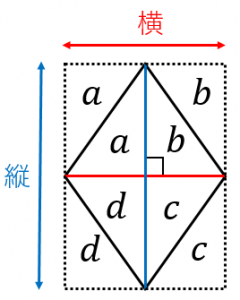
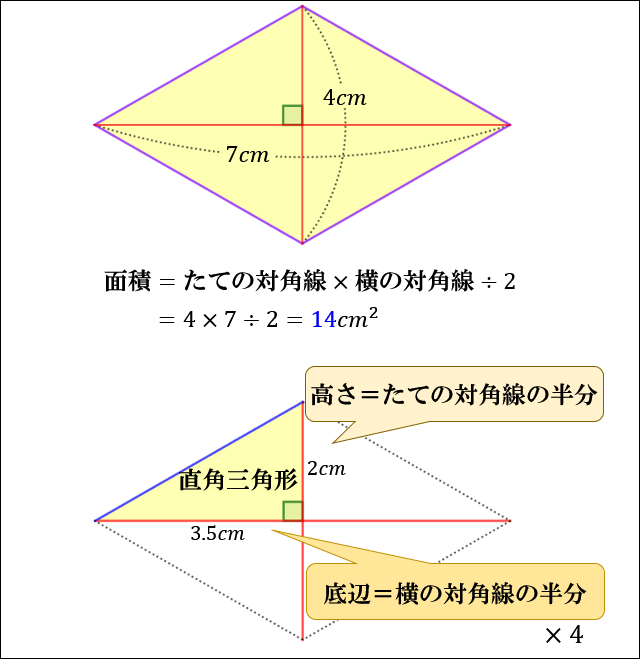
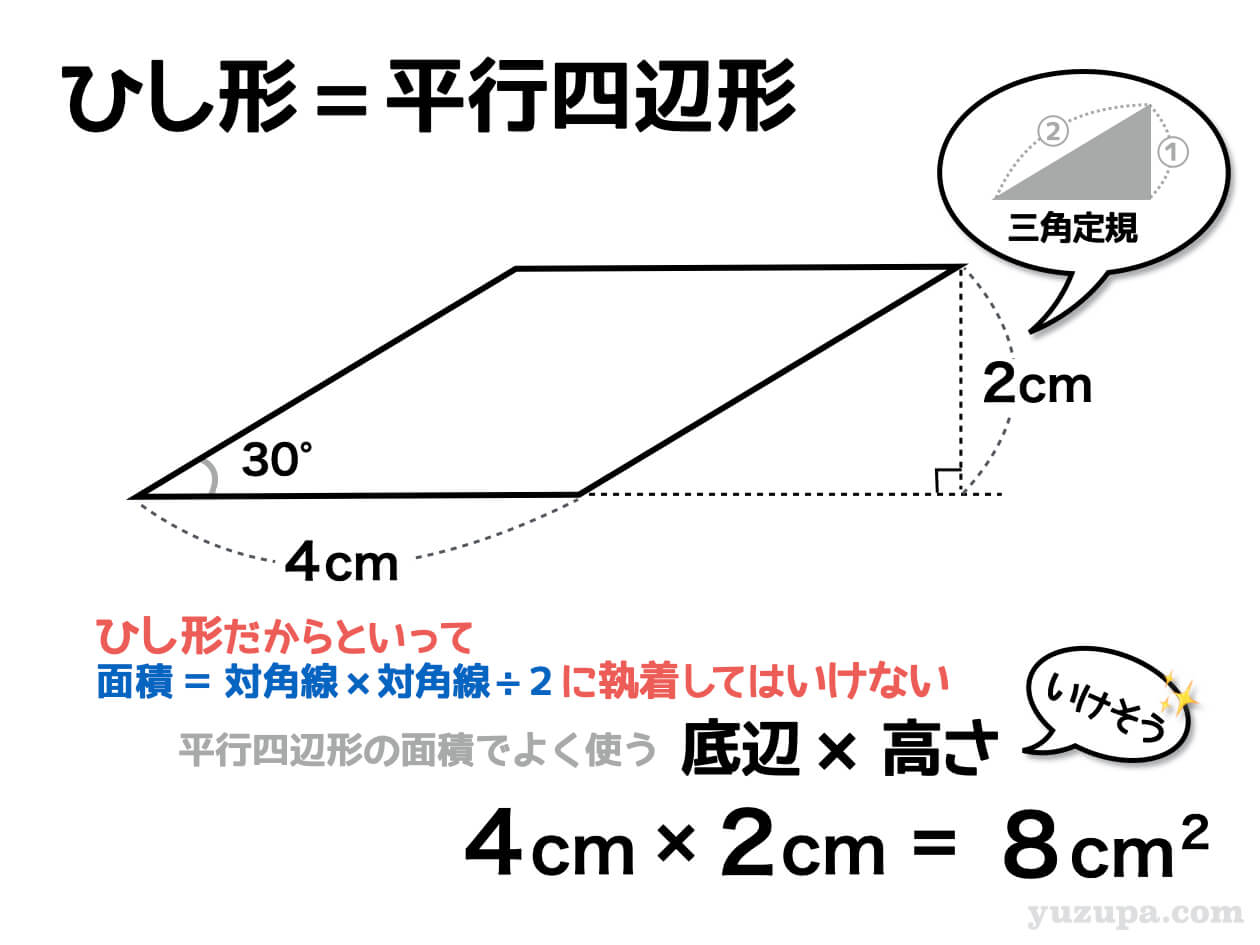
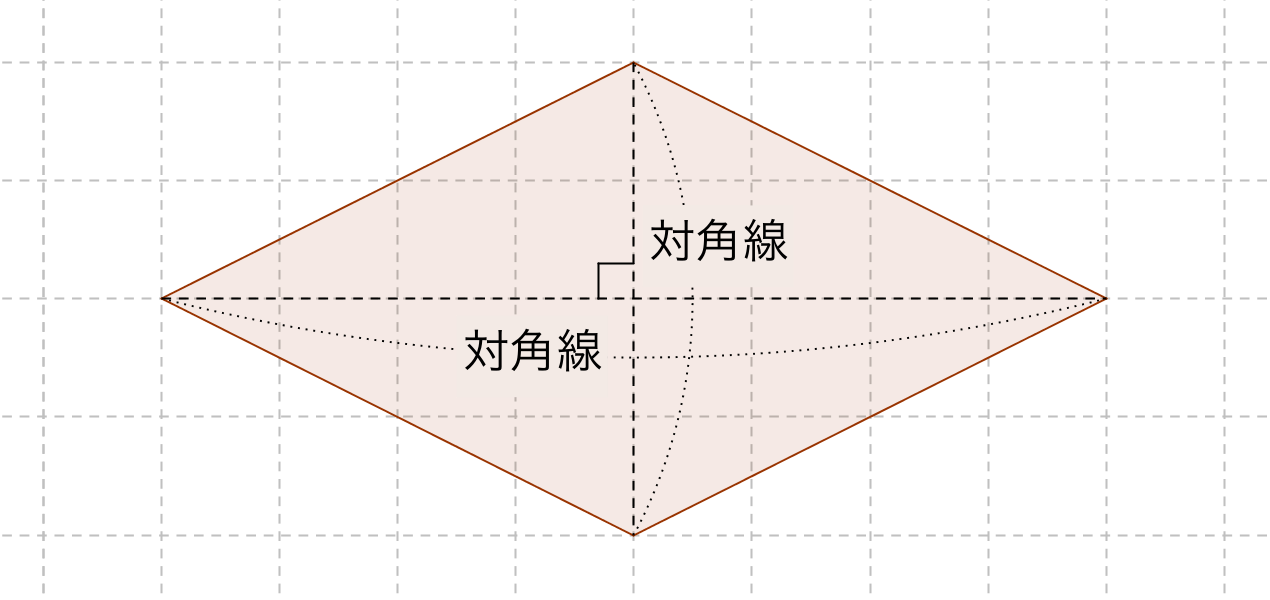
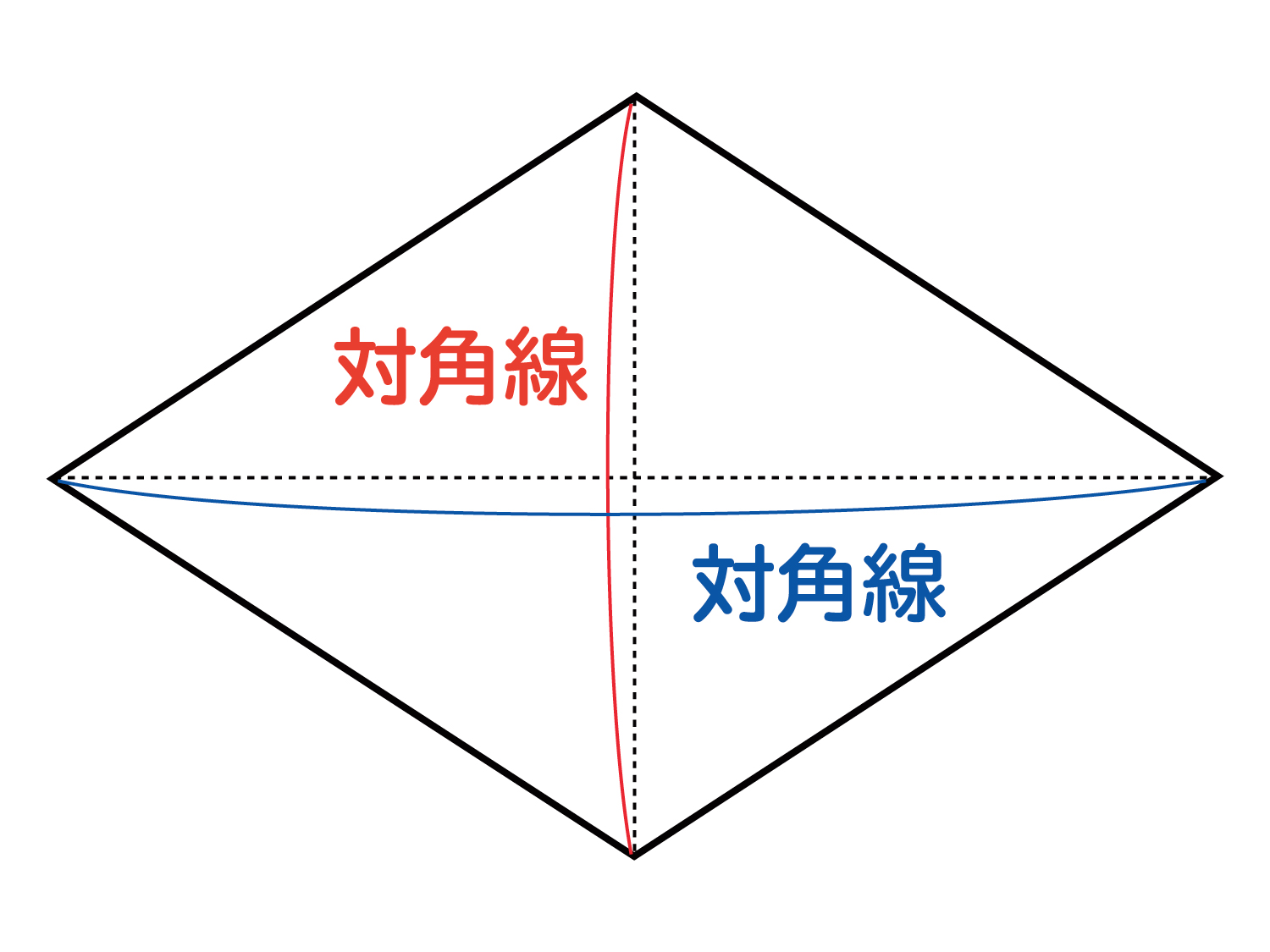
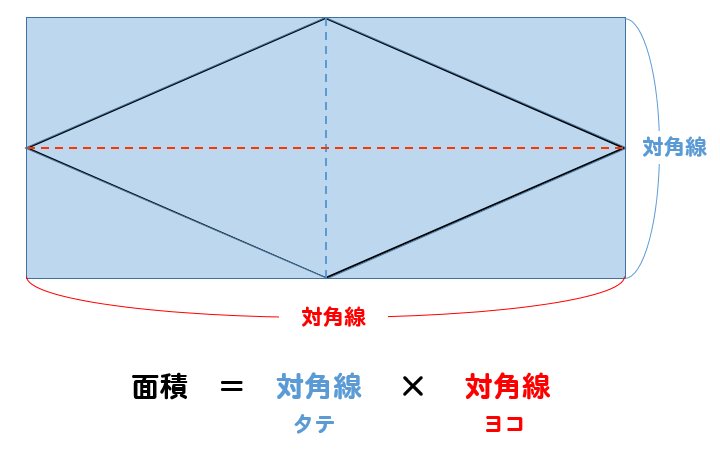
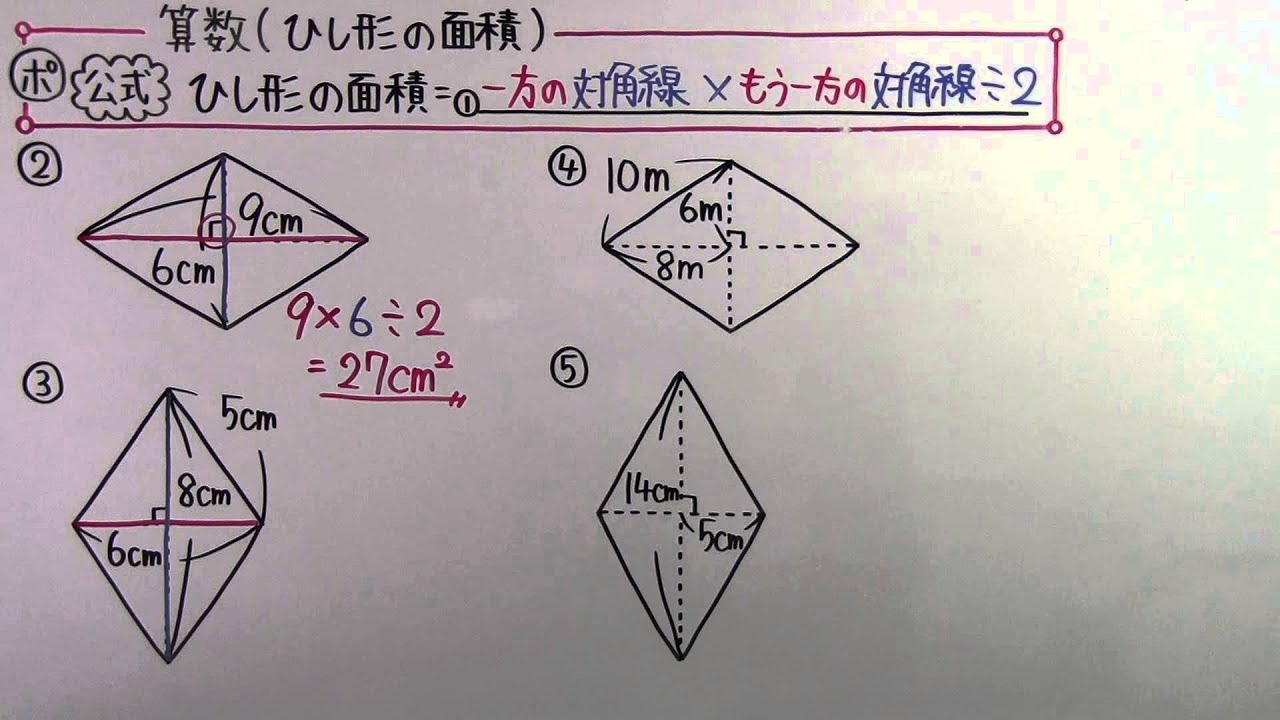
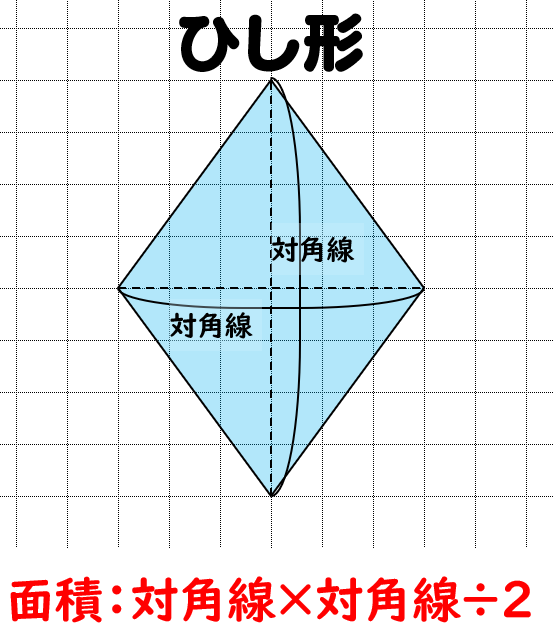
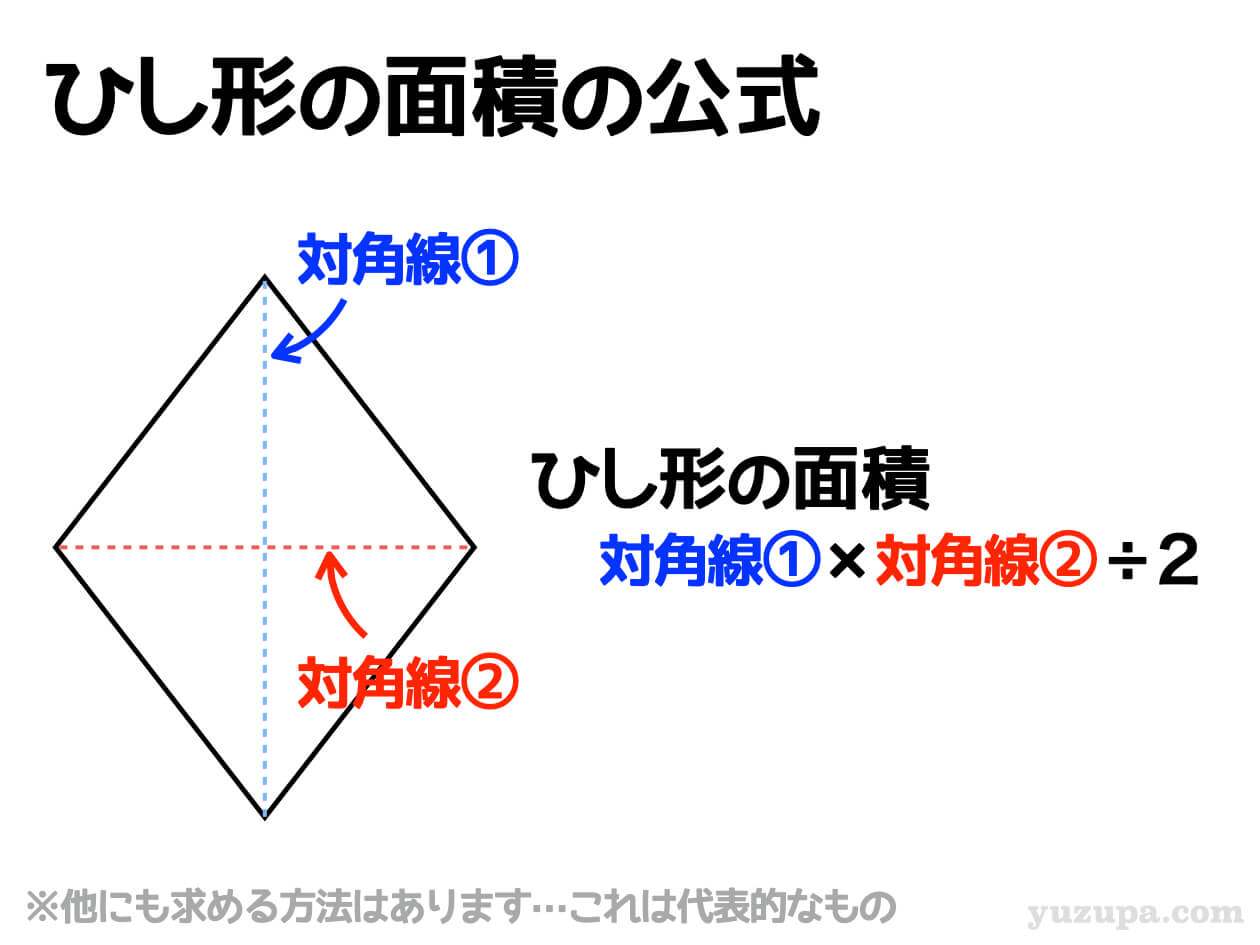
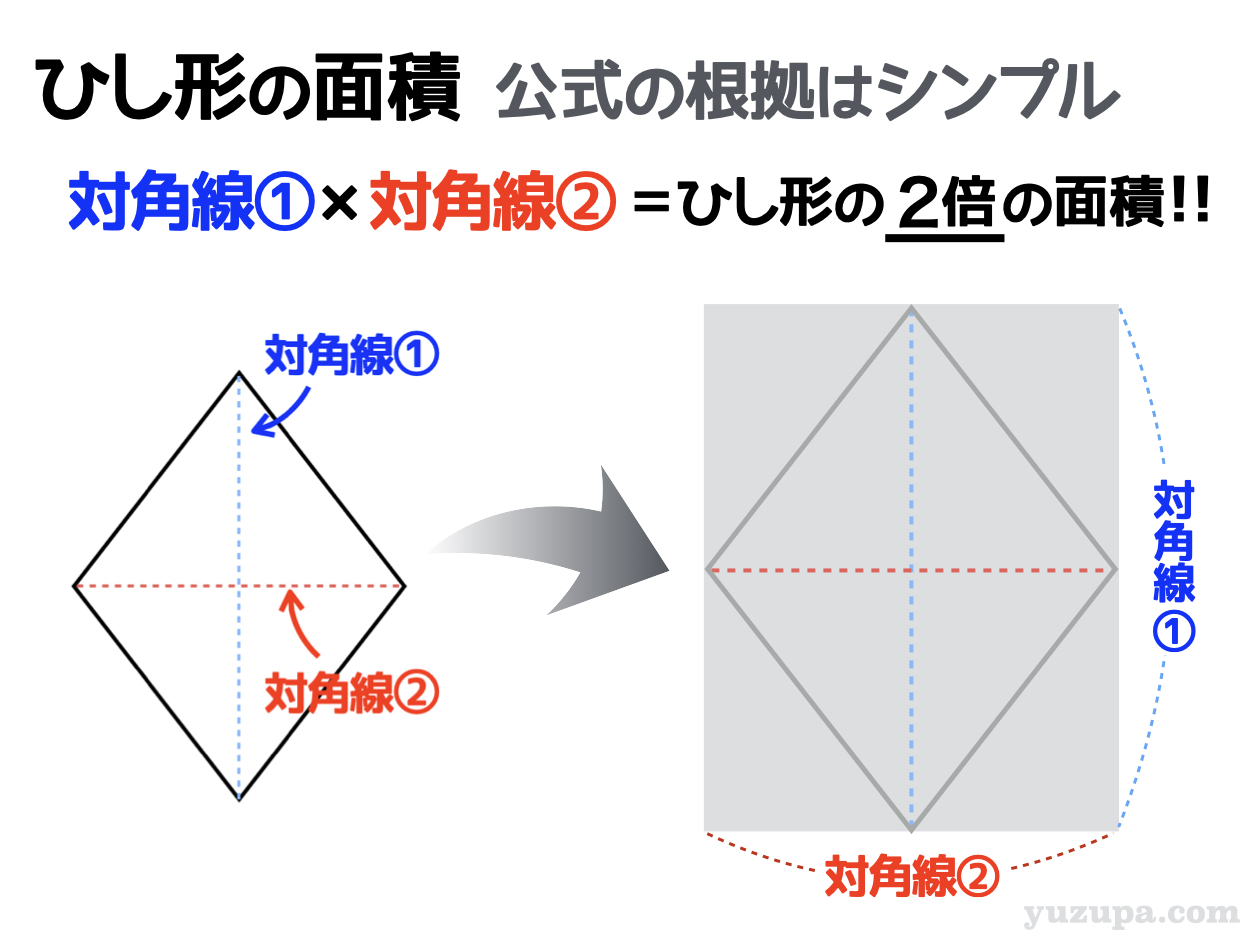
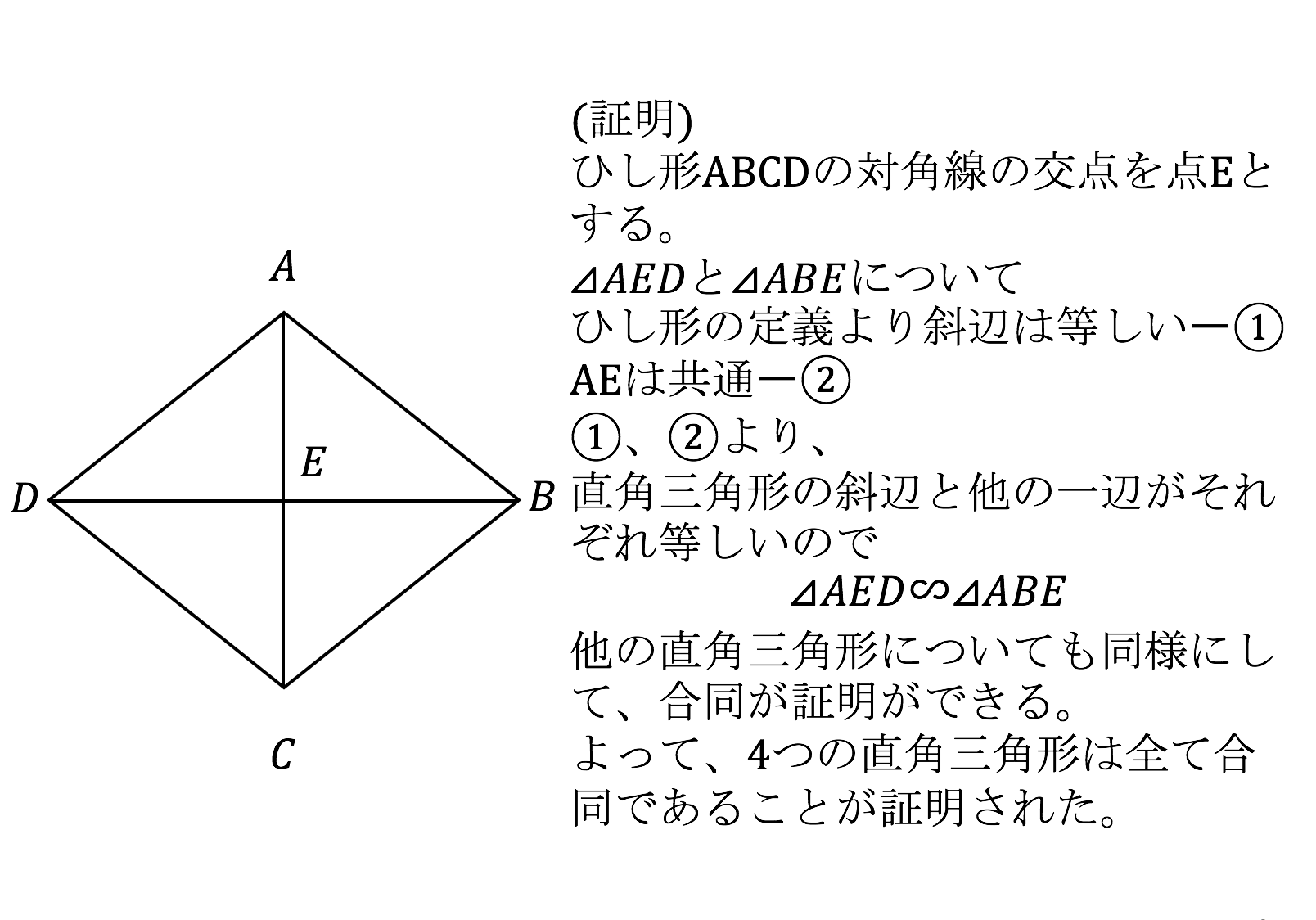
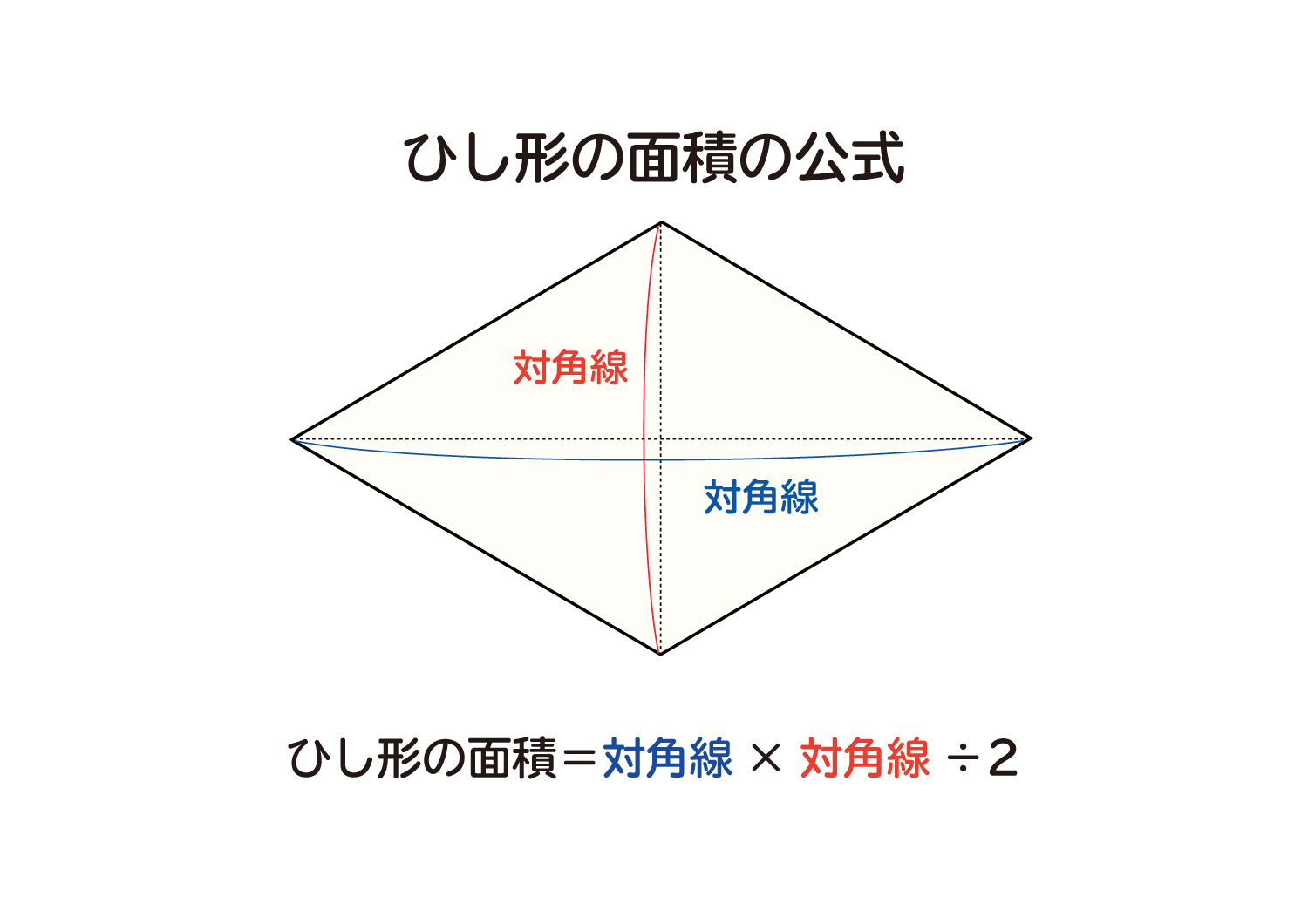
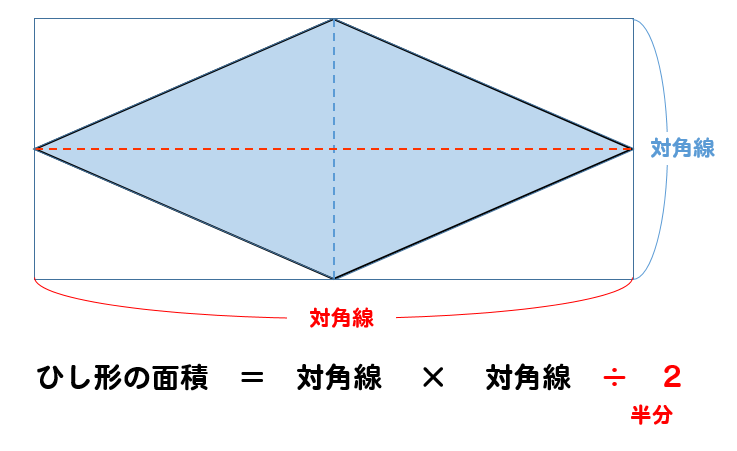
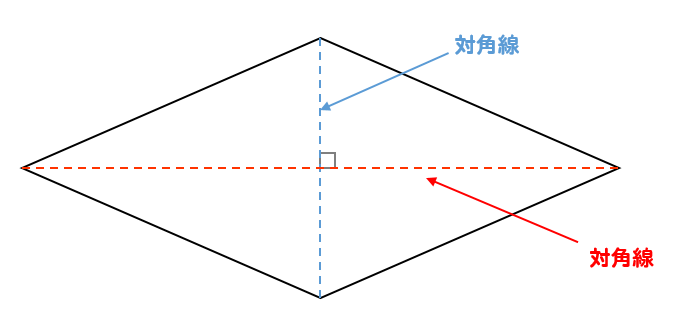
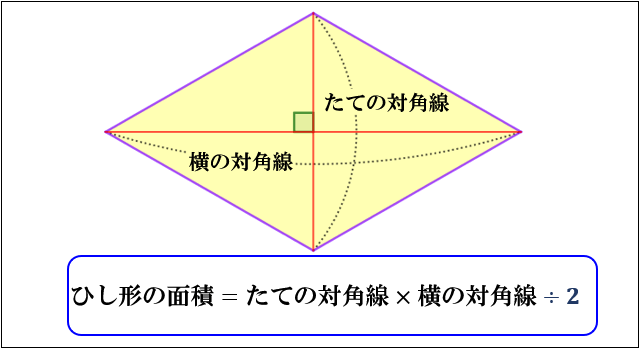
ひし形の面積の公式 対角線×もう一方の対角線÷2 ぼくたちは,長方形や正方形の面積の求め方を習ったよ。でもひし形に なると,どうして対角線どうしをかけたり,2でわったりするの? (例) このひし形を上の図のようにかこむと長方形になります。2712 正方形の対角線の長さの求め方平行四辺形の面積の公式|なぜ『底辺×高さ』で求められるのか? 管理人 9月 17, 18 / 11月 17, 18 向かい合う辺がそれぞれ平行の四角形を『 平行四辺形 ( へいこうしへんけい ) 』と言いますが、平行四辺形の面積は正方形や長方形同様、簡単な計算で
ひし形 面積 求め方 理由
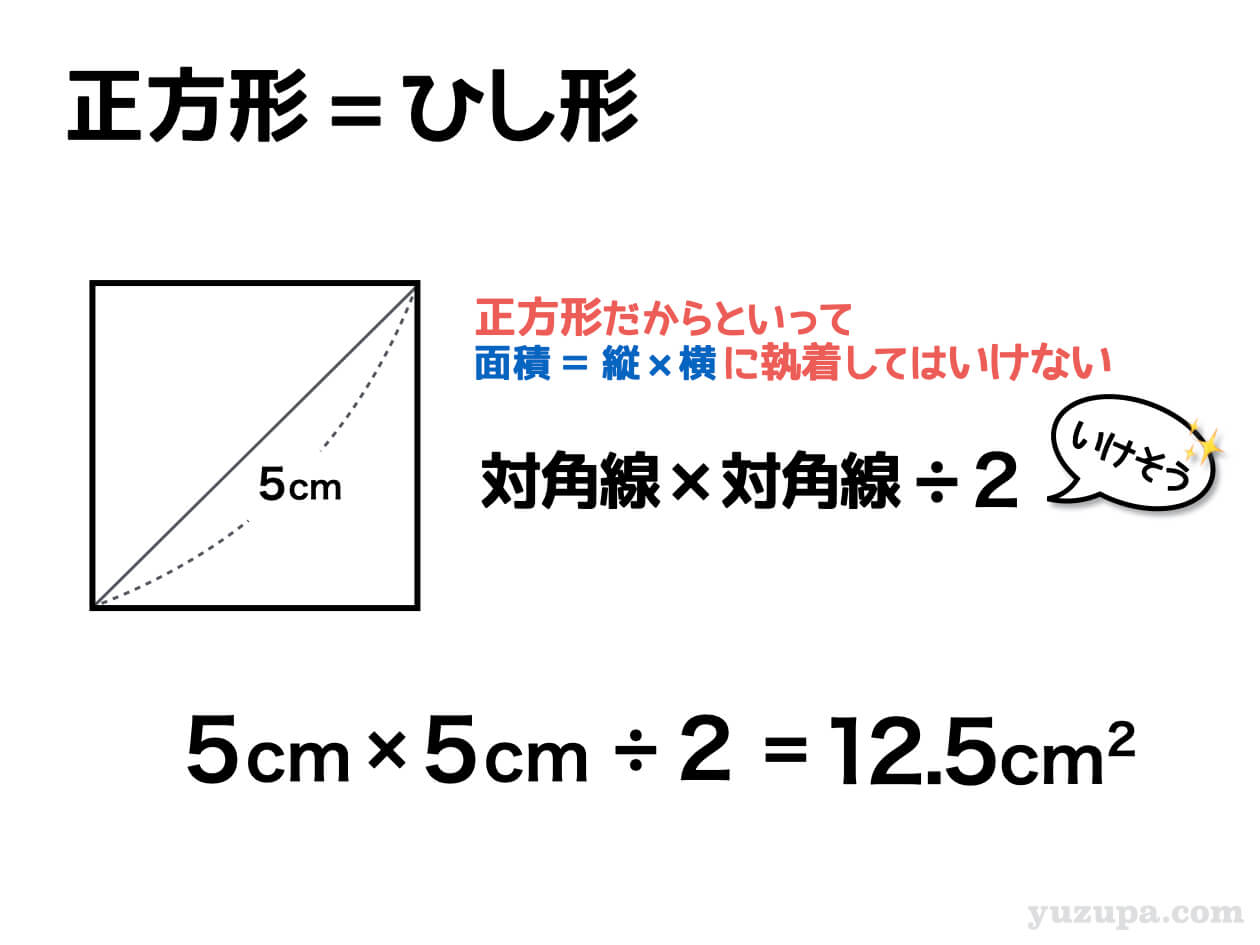
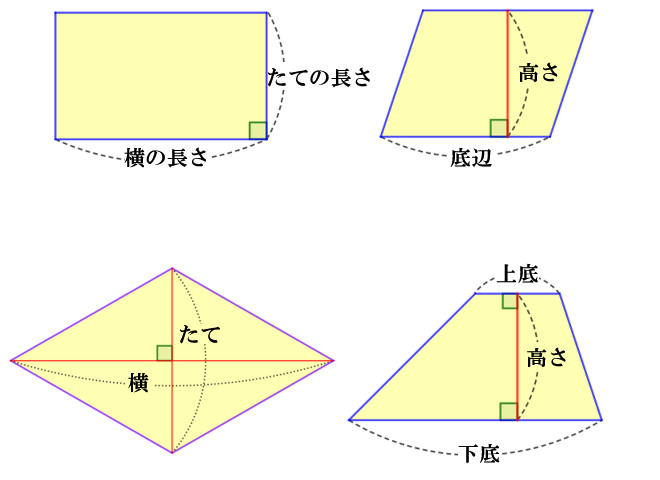
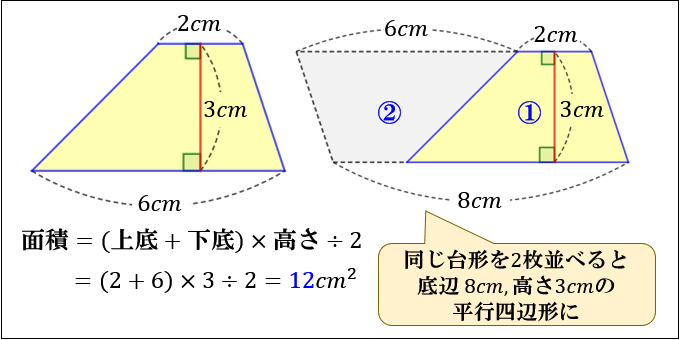
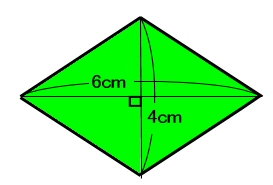
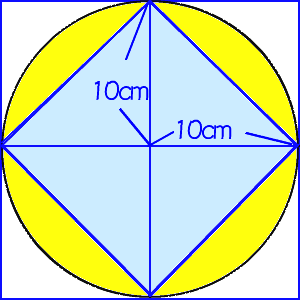
ひし形 面積 求め方 理由- 角度や辺、面積を求めたり、比で表したりします。この単元では、図形の性質と基本公式をしっかり覚えておくことがポイントです。 覚えておきたい面積の求め方は、 四角形(正方形・長方形)、平行四辺形、台形、ひし形、三角形 の5つとなっています。ひし形の面積を求める公式は、s = (縦の対角線)×(横の対角線)÷2 で表されます。このページでは、ひし形の面積の求め方を、計算問題と共に説明しています。また、公式の導き方も説明しています。

簡単公式 ひし形 菱形 の面積を計算できる2つの求め方 Qikeru 学びを楽しくわかりやすく
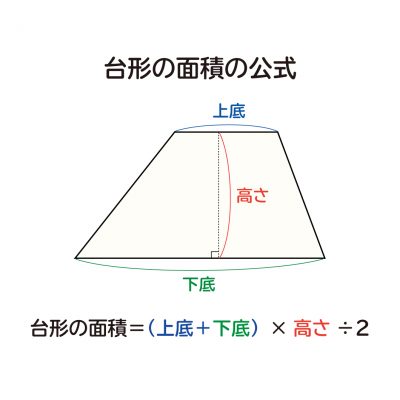
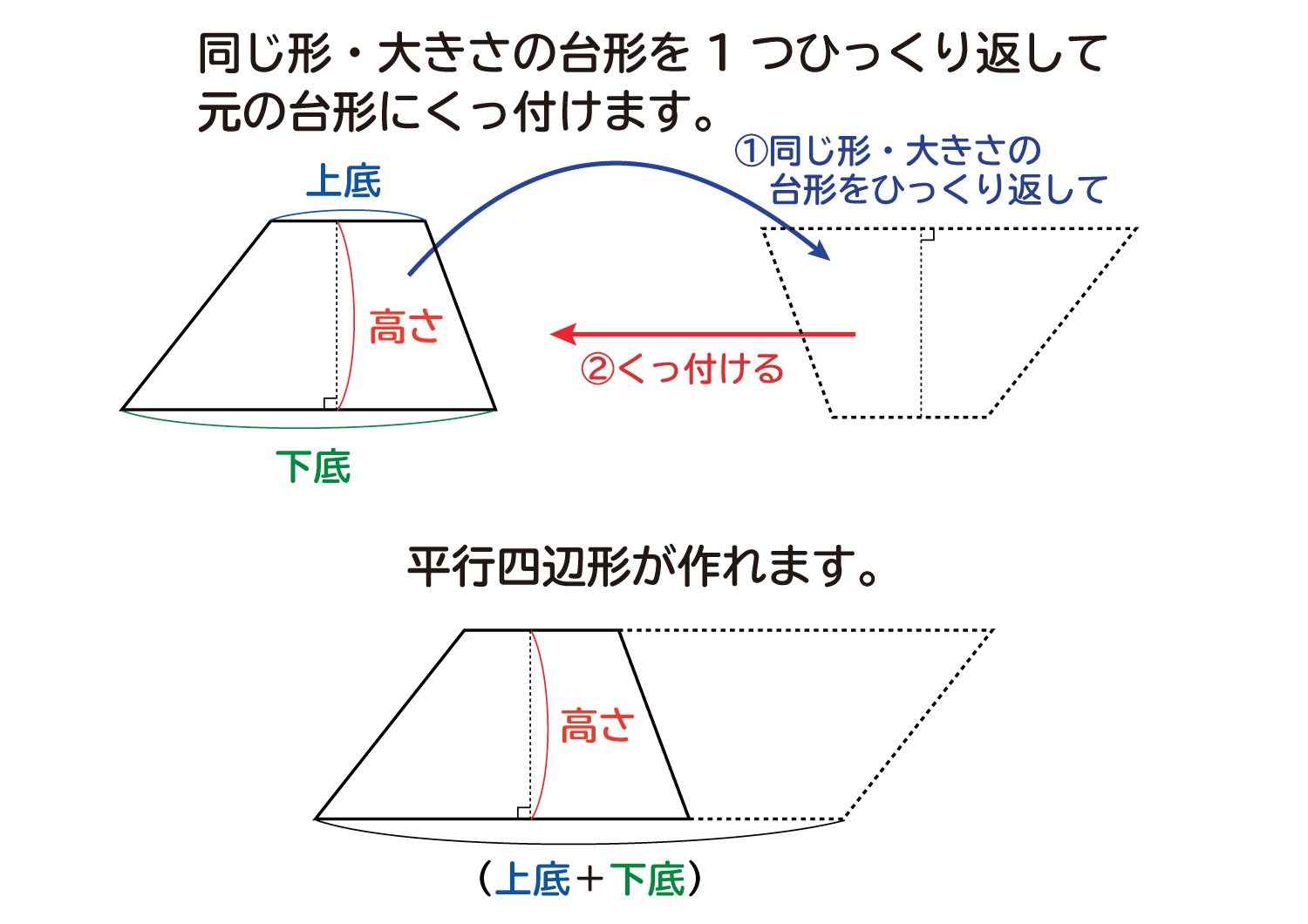
題 ってひし形の面積を求めること ができる。 確実に定着させるために 追 <長方形、正方形、平行四辺形、三角形の面積の求積公式をもと ・平行四辺形や三角形では、ど 究 にして、面積の求め方を考える。> この長さが分かれば公式が使 小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 度数分布表からの平均値の求め方がわかる5ステップ 中3数学 高さがわからない台形の面積の求め方がわかる3ステップ 中3数学 たすきがけ因数分解で二次方程式を解く5つのステップ 中1数学 5年生 1649 up!5年 北海道旭川市立近文小学校 武田 要 1.はじめに ~なぜ「台形の面積の求め方」なのか~ ひし形及び台形の面積の求め方は,今回の学習指導要領の改訂で,5年生に新たに追加された指導内容の1つである。
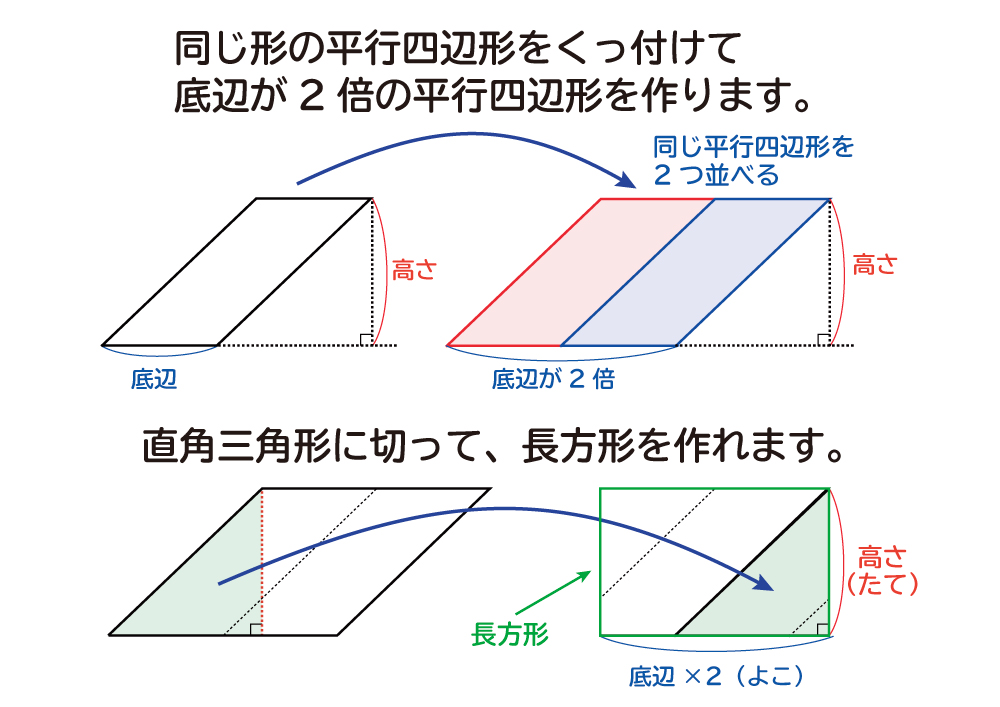
面積の求め方 その理由について、図形を使いながら直観的に理解していきましょう。 まず、図1を見てください。 こちらは (底辺)=2、 (高さ)=3の平行四辺形です。 公式通りに解くと、 2×3=6 ですね。 次に、図2を見てください。 平行四辺形の上に 2本の対角線の長さ a, b と対角線の交わる角度 θ が分かっている場合、その四角形の面積 S は S = 1 2 a b sin θ で求められます。 関連記事 三角関数の基礎知識。 sinθ cosθ tanθ の覚え方・弧度法・三角比の表まとめ たとえば、「2本の対角線の長さが 8既習の面積の公式を基に、三角形、平行四辺形、ひし形及び台形の面積を工夫して求めたり、 公式にまとめたりできる。 (数学的な考え方) 三角形、平行四辺形、ひし形及び台形の面積を求める公式を用いて、面積を求めることができ る。
ひし形 面積 求め方 理由のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 | ||
「ひし形 面積 求め方 理由」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「ひし形 面積 求め方 理由」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「ひし形 面積 求め方 理由」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「ひし形 面積 求め方 理由」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 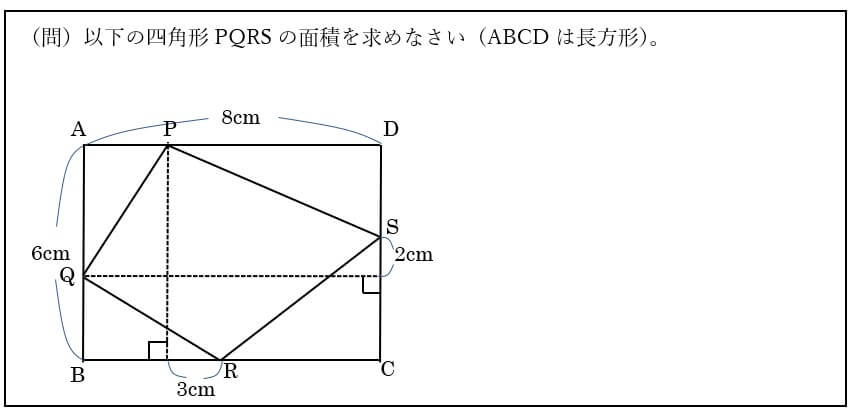 | |
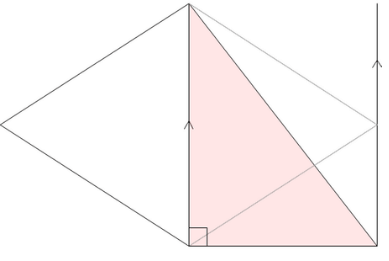 |  |  |
 |  |  |
「ひし形 面積 求め方 理由」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 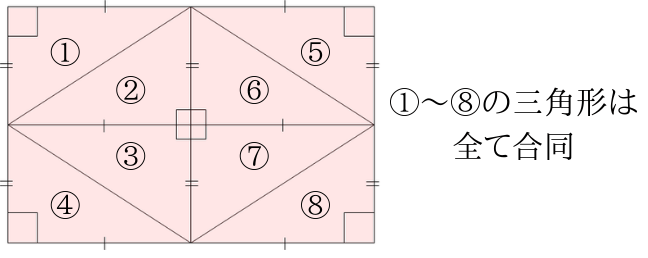 |
 |  | |
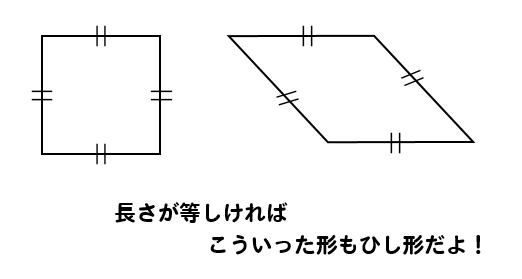 | 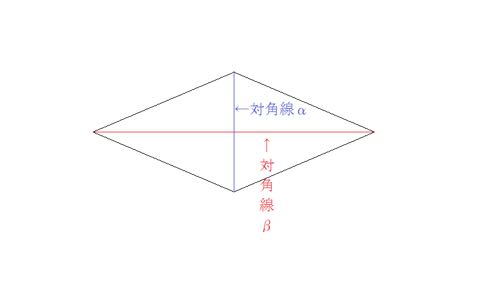 | 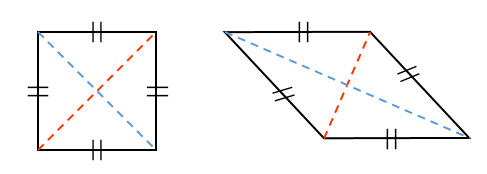 |
「ひし形 面積 求め方 理由」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 | ||
「ひし形 面積 求め方 理由」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「ひし形 面積 求め方 理由」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「ひし形 面積 求め方 理由」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「ひし形 面積 求め方 理由」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「ひし形 面積 求め方 理由」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
し形の性質,かき方 〔6 の面積の求め方 単元観 する活動を多く取り入れる。また, (1)図形の面積を計算によって求めることができるようにする。 ア 三角形,平行四辺形,ひし形及び台形の面積の求め方を考えること。三角形の面積は求めることができるが,「台形の面積の求め方はどうすればよいのか?」という課題意識を高めることができる。 3.具体的な授業の流れ (1)本時の目標 台形の面積の求め方について考え,説明することができる。 (2)本時の展開





0 件のコメント:
コメントを投稿